Network Sparsity
05 Nov 2017This article is about some methods to sparsify neural network by training.
Recently I have read two paper published by Sung Ju Hwang group in ICML 2017. I think these two papers share some ideas. Put them here to be compared.
Combined Group and Exclusive Sparisty for Deep Neural Network
Paper in one sentence
This paper adds two regularizers: Group sparsity and exclusive sparsity, to train neural network.
Motivation
- In the optimal case, the weights at each layer will be fully orthogonal to each other, and thus forming an orthogonal basis set.
- To do so, enforce network weights at each layer to fit to different sets of input features as much as possible. (exclusive sparsity)
- However, it is not practical nor desirable to restrict each weight to be completely disjoint from others as some features still need to be shared (think about low level features). Therefore introduce an additional group sparsity regularizer based on (2, 1)-norm. (group sparsity)
Idea Visiualization
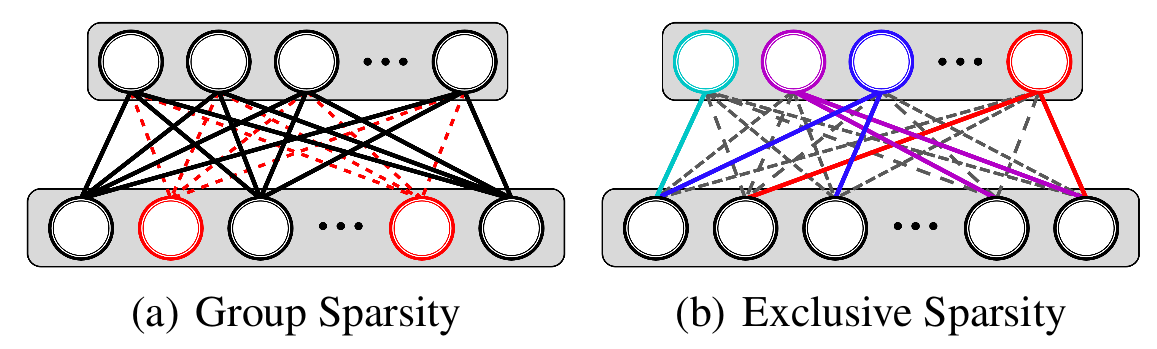
- Group Sparsity tries to delete input neurons.
- Exclusive Sparsity tries to make output neurons fight for input neurons. That is to say input neurons belong to only one output neuron.
Formulation
Group Sparsity
\(\Omega (\mathbf{W}) = \sum_g ||\mathbf{W}_g^l||_2 = \sum_g \sqrt{\sum_i (w_{g,i}^l)^2}\)
where:
- \(g\) represents group, in this paper, every input neuron and its corresponding weights are a group.
- \(l\): layer of neural network
Obviously we can see, it does a group lasso in input neuron: do 2-norm at group first, then do 1-norm between groups.
Exclusive Sparsity
\(\Omega (\mathbf{W}) = \frac{1}{2} \sum_g ||\mathbf{W}_g^l||_1^2 = \frac{1}{2} \sum_g (\sum_i |w_{g,i}^l|)^2\)
Some thinkings
It is easy to knwo using group lasso can result in group sparsity. But it confuses me why using (1,2)-norm can “make output neurons compete for inputs”.
As is said in paper:
Applying 2-norm over these 1-norm groups will result in even weights among the groups; that is, all groups should have similar number of non-sparse weights, and thus no group can have large number of non-sparse weight.
Also, exclusive sparsity was first introduced in Multi-task learning: Hierarchical Classification via Orthogonal Transfer Maybe can find more details in this paper.
Optimization
It uses Proximal Gradient Descent:
- First obtains the intermediate solution \(\mathbf{W}_{t+\frac{1}{2}}\) by taking a gradient step using the gradient computed on the loss only.
- Then optimize for the regularization term while performing Euclidean projection of it to the solution space: \(\min_{\mathbf{W}_{t+1}} = \{\Omega (\mathbf{W}_{t+\frac{1}{2}}) + \frac{1}{2\lambda} || \mathbf{W}_{t+1} - \mathbf{W}_{t+\frac{1}{2} }||_2^2 \}\)
Group Sparsity proximal step
Set \(f(\mathbf{W}_{t+1}) = \frac{1}{2} ||\mathbf{W}_{t+1} - \mathbf{W}_{t + \frac{1}{2}}||^2_2 + \underbrace{\lambda [\mathbf{W}_{t+ 1}^1, \mathbf{W}_{t+ 1}^2, ... ,\mathbf{W}_{t+ 1}^g]}_{\text{Regularizer}}\)
\[\frac{\partial f(\mathbf{W}_{t+1})}{\partial \mathbf{W}_{t+1}} = \mathbf{W}_{t+1} - \mathbf{W}_{t + \frac{1}{2}} + \lambda [\frac{\mathbf{W}_{t+1}^1}{||\mathbf{W}_{t+1}^1||_2}, \frac{\mathbf{W}_{t+ 1}^2}{||\mathbf{W}_{t+ 1}^2||_2}, ... ,\frac{\mathbf{W}_{t+ 1}^g}{||\mathbf{W}_{t+ 1}^g||}] = 0\]Finally we get: \(\mathbf{W}^{t+1}_{g,i} = \left(1 - \frac{\lambda}{||\mathbf{W}_g||_2} \right)_{+} \mathbf{W}^{t + \frac{1}{2}}_{g,i}\)
Exclusive Sparsity
\(\mathbf{W}^{t+1}_{g,i} = \left(1 - \frac{\lambda ||\mathbf{W}_g||_1}{|w_{g,i}|} \right)_{+} \mathbf{W}^{t+\frac{1}{2}}_{g,i}\)
Experiments
Visualization–Fully Connected

- Group sparsity regularizer results in the total elimination of certain features.
- Exclusive sparsity regularizer, when used on its own, results in disjoint feature selection for each class.
- When combined, it allows certain degree of feature reuse
Visualization–Convolution
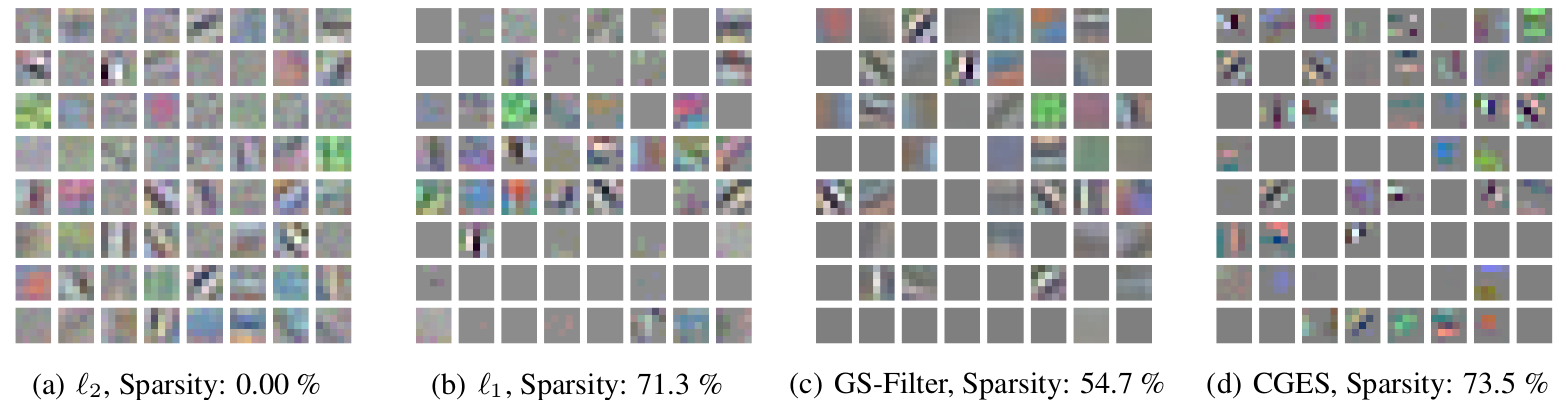
- Combined group and exclusive sparsity regularizer results in filters that are much sharper than others.
- Some spatial features dropped altogether from the competition with other filters.